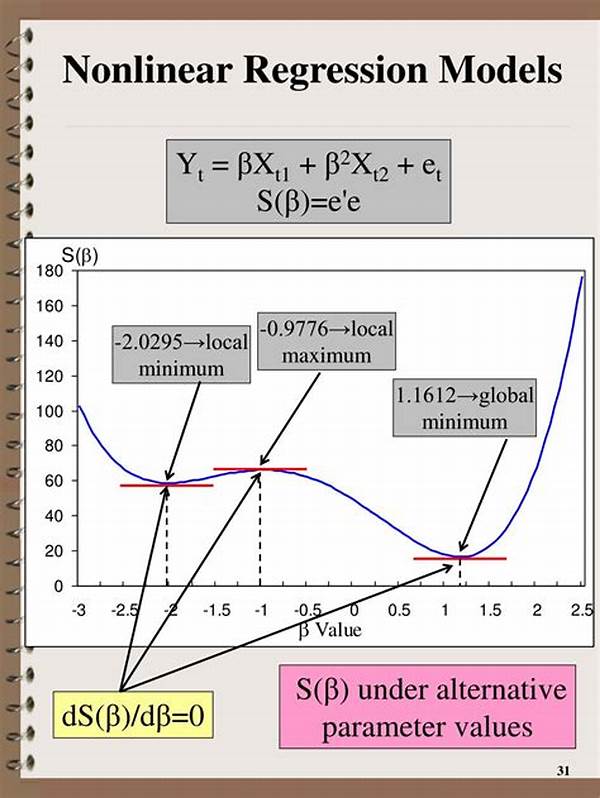
The study of nonlinear models for scientific data has increasingly become a focal point in modern-day research. These models are essential for understanding complex phenomena that cannot be captured by linear assumptions. Nonlinear models are instrumental in elucidating the intricacies present in various scientific datasets, ranging from biology and chemistry to economics and physics. Their ability to model real-world scenarios more faithfully than linear models makes them indispensable in certain areas of research. In this article, we will delve into their application, advantages, and the nuances that make them crucial for scientific exploration.
Read Now : Efficient Database Indexing Strategies
The Importance of Nonlinear Models in Scientific Research
Nonlinear models for scientific data hold substantial importance across numerous fields of research. These models offer significant versatility and provide a more accurate representation of natural processes that often involve complex interdependencies. Traditional linear models may fall short in capturing the subtleties of these processes, as they rely on the assumption of constant proportionality. Conversely, nonlinear models encapsulate the dynamic nature of scientific phenomena, allowing scientists to simulate environmental changes, chemical reactions, and biological growth patterns more effectively.
In understanding this significance, one must recognize the application of nonlinear models in modeling chaotic systems. These systems are inherently unpredictable, and yet, nonlinear models for scientific data can provide approximations that offer valuable insights. They serve as a basis for predicting ecosystem dynamics, weather patterns, and financial market behaviors. Moreover, these models facilitate the study of bifurcation, feedback loops, and other complex behaviors that linear models cannot adequately address. For researchers and practitioners aiming for precision and depth, nonlinear models become an essential toolkit.
A further advantage of nonlinear models for scientific data lies in their ability to handle large and complex datasets. With technological advancements, the volume of data available to researchers has exploded, and only robust models have the capacity to decipher this information effectively. Machine learning algorithms, many of which employ nonlinear modeling techniques, are at the forefront of scientific discovery. Their integration into research allows for a deeper understanding of underlying patterns and relationships that were previously obscured. As research methodologies evolve and datasets grow in complexity, nonlinear models continue to be indispensable for gaining actionable insights.
Characteristics of Nonlinear Models for Scientific Data
1. Complex Interactions: Nonlinear models for scientific data express complex interactions between variables, often involving multiple parameters that make their behavior multifaceted.
2. Adaptive Flexibility: They provide the flexibility needed to adapt to real-world data complexities where linear models often fail to capture the essence of the phenomena.
3. Predictive Accuracy: By accommodating intricate patterns within datasets, nonlinear models tend to offer greater predictive accuracy than their linear counterparts.
4. Versatile Applications: These models are used in various fields, from ecological modeling to financial forecasting, showcasing their versatile applicability.
5. Handling of Nonlinear Relationships: Nonlinear models adeptly handle relationships where outputs are not proportional to inputs, such as exponential decay, logistic growth, or oscillatory behavior.
Nonlinear Models and Their Computational Requirements
One significant consideration when dealing with nonlinear models for scientific data is their computational demands. These models often require more sophisticated mathematical techniques and powerful computational tools to solve. The complexity of the algorithms used in nonlinear modeling is, in part, due to the non-uniqueness of solutions and the potential for multiple equilibrium states. Consequently, computational efficiency and resource allocation are crucial.
Applications of nonlinear models in high-stakes research scenarios necessitate careful selection of algorithms and optimization techniques. The refinement of these models often involves iterative methods, sensitivity analyses, and robustness checks to maintain the validity and reliability of outcomes. Despite the intricacy, the advancements in computational power and the development of specialized software have made it feasible for scientists to implement nonlinear models for scientific data effectively.
Moreover, researchers must keep abreast of technological advancements to harness the full potential of these models. Innovations in parallel computing, cloud-based platforms, and data visualization tools are pivotal in enhancing the usability and efficiency of nonlinear modeling techniques. As computational resources continue to grow, so too does the scope and complexity of problems that can be tackled with nonlinear models, enabling groundbreaking discoveries across disciplines.
Advanced Techniques in Nonlinear Modeling
Nonlinear models for scientific data have benefitted from sophisticated statistical and computational advancements. Here are ten explanations of these techniques:
1. Differential Equations: Often used in nonlinear models to describe dynamic processes involving rates of change.
2. Chaos Theory: Applies to systems where sensitivity to initial conditions can lead to drastically different outcomes.
3. Machine Learning Integration: Nonlinear models are increasingly integrated with machine learning techniques to process vast datasets.
4. Optimization Algorithms: Algorithms like genetic algorithms and simulated annealing optimize nonlinear model parameters.
5. Monte Carlo Simulations: These are used to approximate the probability of outcomes in systems with random variables.
Read Now : Agricultural Climate Risk Assessment
6. Sensitivity Analysis: A method to determine how different variables affect the outcomes of nonlinear models.
7. Robust Statistical Methods: Employed to handle data noise and outliers in nonlinear datasets.
8. Bayesian Networks: They provide a probabilistic approach to modeling complex systems with uncertain data.
9. Phase Space Analysis: This technique helps visualize trajectories of dynamical systems in nonlinear models.
10. Numerical Simulations: Implemented to solve nonlinear equations that have no analytical solutions.
The Evolution of Nonlinear Models in Modern Science
The evolution of nonlinear models for scientific data is intertwined with advancements in science and technology. These models have transformed from rudimentary mathematical formulations to sophisticated tools integral to scientific inquiry. In the past, linear models dominated the analytical landscape due to their simplicity and ease of interpretation. However, as complexities in scientific data became evident, the limitations of linear models paved the way for nonlinear approaches.
During the late 20th century, an increased focus on system dynamics, chaos theory, and complex adaptive systems catalyzed the development of non-linear methodologies. The recognition that small changes in initial conditions could produce vastly different outcomes highlighted the need for models that embrace complexity rather than reduce it. With computational power on the rise, researchers began to incorporate more variables and complex relationships into their models, thus enhancing their predictive capabilities.
In contemporary science, the proliferation of data-driven research has reinforced the necessity for nonlinear models. The real-time processing capabilities afforded by modern computing enable researchers to test hypotheses and validate models quicker and with unparalleled precision. Importantly, interdisciplinary collaboration has broadened the application of nonlinear models, allowing for innovations such as predictive climate models, holistic healthcare systems, and intelligent robotic systems. These developments not only underscore the critical nature of nonlinear models but also open up new horizons for what scientific research can achieve.
Applications and Challenges of Nonlinear Models
In the ever-expanding realm of scientific research, nonlinear models for scientific data emerge as both powerful tools and complex challenges. Their applications span across diverse fields, including ecology, where they help model predator-prey dynamics, and economics, improving predictions of market fluctuations. Similarly, in neuroscience, these models facilitate understanding intricate neural networks’ functionality.
The challenges, however, reside in the inherent complexity and computational intensity associated with nonlinear models. Developing highly accurate nonlinear models is an iterative process that demands expertise in mathematics, domain-specific knowledge, and advanced computational resources. Often, the non-uniqueness of solutions and potential instability require meticulous validation and verification procedures.
Nonetheless, the promise of nonlinear models for scientific data is undeniable. They enable scientists to gain deeper insights into complex systems, unravel previously undetected patterns, and propose evidence-based solutions to multifaceted problems. Their evolving nature invites continuous research and innovation, setting a trajectory for future breakthroughs across scientific domains.
Conclusion: The Future Trajectory of Nonlinear Models
In conclusion, nonlinear models for scientific data are indispensable components of contemporary scientific endeavors. Their capacity to model complex, real-world phenomena with precision and adaptability ensures their continued relevance and importance. As computational technologies progress and the volume and complexity of data expand, the reliance on nonlinear models is expected to intensify.
The adoption and integration of these models in modern research signify a paradigmatic shift towards embracing complexity and uncertainty. The challenges accompanying nonlinear models are met with continual improvements in algorithms, computational resources, and interdisciplinary collaboration. Through these efforts, researchers are empowered to explore innovative solutions to some of the most pressing scientific questions facing society today.
As we look to the future, the role of nonlinear models for scientific data is poised to further revolutionize fields beyond traditional boundaries. With continued advancements, these models promise to unlock new dimensions of understanding and unlock innovations across a spectrum of disciplines, driving forward the frontiers of scientific discovery.